In case you're unfamiliar with the diffraction limit, for telescopes it says that the ultimate limit for angular resolution is a function of the used wavelength and diameter of the used focusing element. For a microscope their resolution is a function of the wavelength and the index of refraction. That's why astronomical telescopes tend to be huge and microfabrication uses shorter wavelengths.
We already knew superlenses existed, but they were mostly limited to near field. Spatial-mode demultiplexing on the other hand can be utilized to beat the diffraction limit in the far field as well. While not entirely surprising, it's not everyday news. I can't wait to buy a telescope that allows me to see the footprints on the moon (likely not going to happen anytime soon).
This method has some similarities to Fourier transforms in a way that is decomposes the spatial modes of the electromagnetic field into orthogonal components that not only carry information about the amplitude, but phase as well.
 |
| Here's an unrelated figure. |
https://arxiv.org/pdf/1608.03211v1.pdf
"The seemingly infinite enhancement offered by SPADE does not imply unlimited resolution for finite photon numbers. Provided that enough photons can be collected, however, the giant improvements over direct imaging should still be useful."
Far-field linear optical super-resolution via heterodyne detection in a higher-order local oscillator mode
https://arxiv.org/pdf/1606.02662v2.pdf
"If our technique is used with state-of-the art microscopes, precision on nanometer scales can be expected."
Achieving the ultimate optical resolution
https://doi.org/10.1364/OPTICA.3.001144
"Our results stress that diffraction resolution limits are not a fundamental constraint but, instead, the consequence of traditional imaging techniques discarding the phase information."
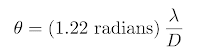


No comments:
Post a Comment